Selected Publications

More Publications

We study projection-free methods for constrained Riemannian optimization. In particular, we propose the Riemannian Frank-Wolfe (RFW) method. We analyze non-asymptotic convergence rates of RFW to an optimum for (geodesically) convex problems, and to a critical point for nonconvex objectives. We also present a practical setting under which RFW can attain a linear convergence rate. As a concrete example, we specialize RFW to the manifold of positive definite matrices and apply it to two tasks: (i) computing the matrix geometric mean (Riemannian centroid); and (ii) computing the Bures-Wasserstein barycenter. Both tasks involve geodesically convex interval constraints, for which we show that the Riemannian “linear oracle” required by RFW admits a closed form solution. We demonstrate numerically that RFW performs competitively in comparison with state-of-the-art Riemannian optimization methods.
Under Review, 2021.
Preprint Code Project Video

We consider a simple control problem in which the underlying dynamics depend on a parameter that is unknown and must be learned. We exhibit a control strategy which is optimal to within a multiplicative constant. While most authors find strategies which are successful as the time horizon tends to infinity, our strategy achieves lowest expected cost up to a constant factor for a fixed time horizon.
Rev. Mat. Iberoamericana, 2021.
Preprint Project

We study stochastic projection-free methods for constrained optimization of smooth functions on Riemannian manifolds, i.e., with additional constraints beyond the parameter domain being a manifold. Specifically, we introduce stochastic Riemannian Frank-Wolfe methods for nonconvex and geodesically convex problems. We present algorithms for both purely stochastic optimization and finite-sum problems. For the latter, we develop variance-reduced methods, including a Riemannian adaptation of the recently proposed Spider technique. For all settings, we recover convergence rates that are comparable to the best-known rates for their Euclidean counterparts. Finally, we discuss applications to two classic tasks: The computation of the Karcher mean of positive definite matrices and Wasserstein barycenters for multivariate normal distributions. For both tasks, stochastic Fw methods yield state-of-the-art empirical performance.
IMA Journal of Numerical Analysis, 2021.
Preprint PDF Project

We exhibit optimal control strategies for settings in which the underlying dynamics depend on a parameter that is initially unknown and must be learned. We consider a cost function posed over a finite time interval, in contrast to much previous work that considers asymptotics as the time horizon tends to infinity. We study several different versions of the problem, including Bayesian control, in which we assume a prior distribution on the unknown parameter; and “agnostic” control, in which we assume nothing about the unknown parameter. In the agnostic case, we compare our performance with that of an opponent who knows the value of the parameter. In every case, the optimal strategy turns out to be a Bayesian strategy or a limit of Bayesian strategies.
Rev. Mat. Iberoamericana, 2021.
Preprint

We present, to our knowledge, the first theoretical guarantees for learning a classifier in hyperbolic rather than Euclidean space. Specifically, we consider the problem of learning a large-margin classifier for data possessing a hierarchical structure. Our first contribution is a hyperbolic perceptron algorithm, which provably converges to a separating hyperplane. We then provide an algorithm to efficiently learn a large-margin hyperplane, relying on the careful injection of adversarial examples. Finally, we prove that for hierarchical data that embeds well into hyperbolic space, the low embedding dimension ensures superior guarantees when learning the classifier directly in hyperbolic space.
NeurIPS, 2020.
Preprint PDF Project

The problem of identifying geometric structure in heterogeneous, high-dimensional data is a cornerstone of representation learning. We propose a combinatorial approach to evaluating embeddability, i.e., to decide whether a data set is best represented in Euclidean, Hyperbolic or Spherical space. Our method analyzes nearest-neighbor structures and local neighborhood growth rates to identify the geometric priors of suitable embedding spaces. For canonical graphs, the algorithm’s prediction provably matches classical results. As for large, heterogeneous graphs, we introduce an efficiently computable statistic that approximates the algorithm’s decision rule.
AISTATS, 2020.
Preprint PDF Project Video

Recent Talks

More Talks

Constrained Optimization On Riemannian Manifolds

Nov 29, 2021, Workshop on Optimization Under Symmetry

Riemannian Frank-Wolfe Methods with Applications

Oct 25, 2021, INFORMS Annual Meeting

Frank-Wolfe Methods for efficient geodesically convex optimization

Oct 23, 2021, AMS Fall Sectional Meeting

Geometric Methods for Machine Learning and Optimization

Jun 15, 2021, Oxford Data Science Seminar

Riemannian Frank-Wolfe Methods

May 20, 2021, SIAM Conference on Applied Linear Algebra (Minisymposium: Linear Algebra and Differential Geometry)

Selected Projects

Learning to Control with Little Data

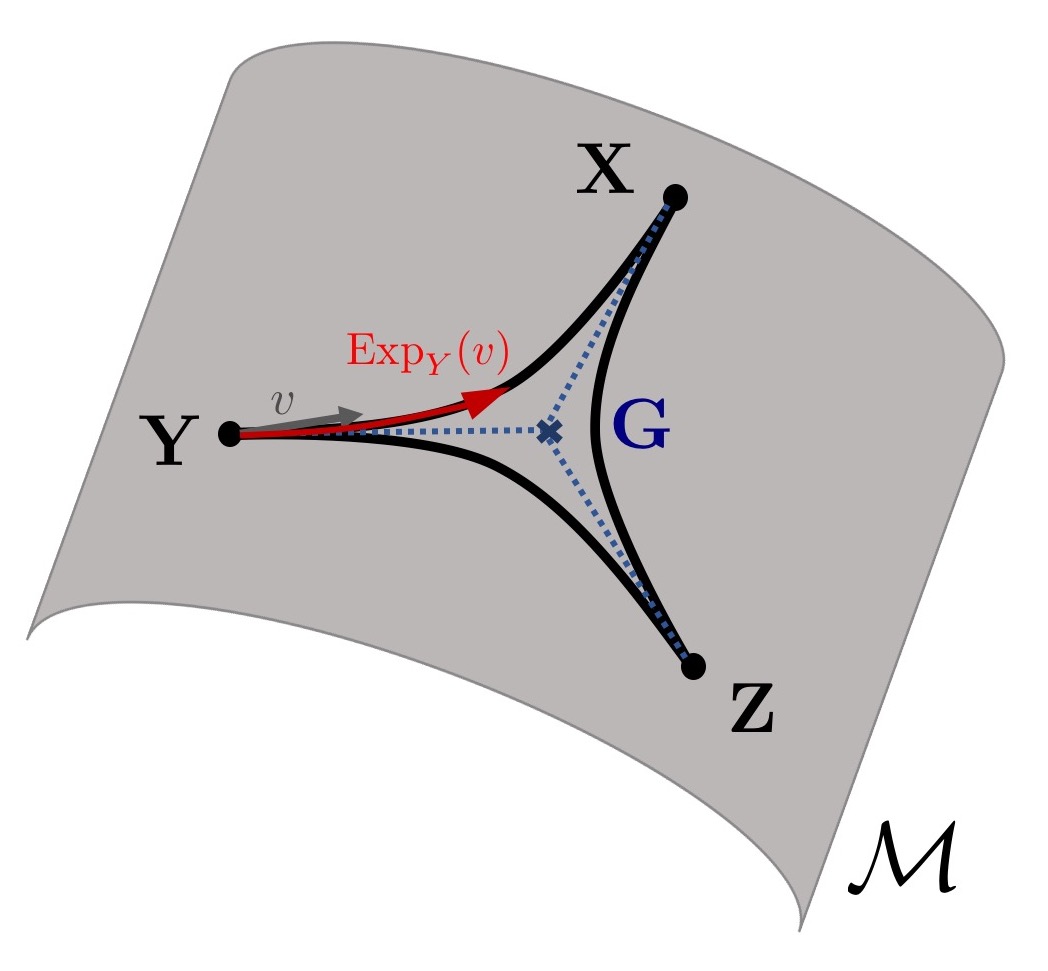
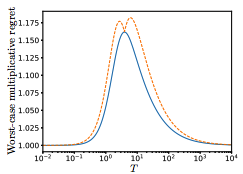
Constrained Optimization on Manifolds

Riemannian Frank-Wolfe methods for nonconvex and g-convex optimization.

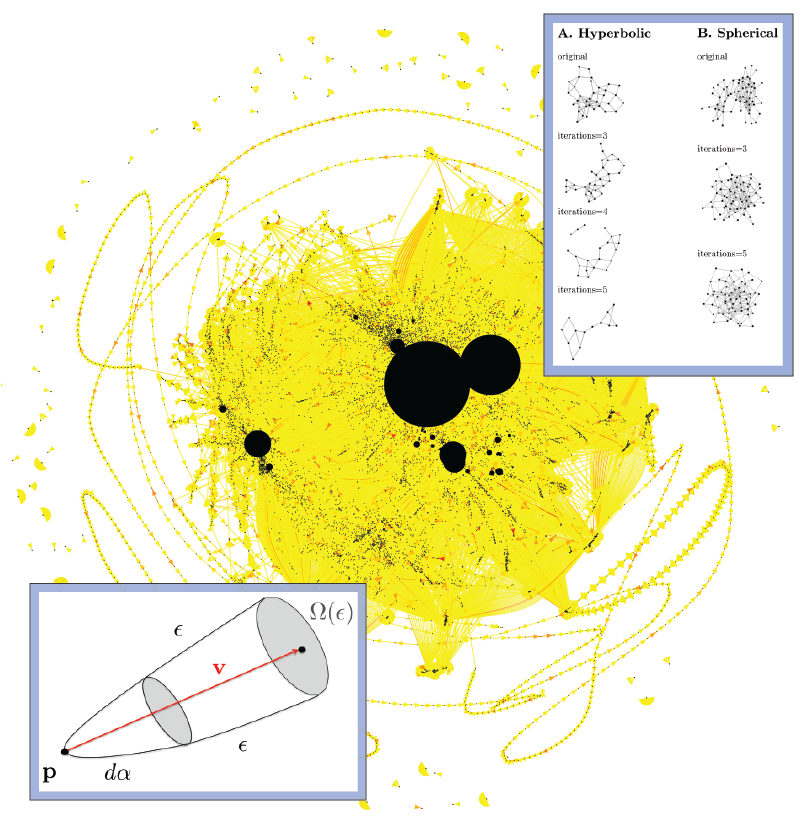
Discrete Geometry and Machine Learning on Graphs

Discrete Ricci curvature for a curvature-based analysis of complex networks.

Machine Learning in Non-Euclidean Spaces

Harnessing the geometric structure of data in Machine Learning.

Contact