control.tf¶

control.tf(*args)¶

Create a transfer function system. Can create MIMO systems.

The function accepts either 1 or 2 parameters:

tf(sys)

Convert a linear system into transfer function form. Always creates a new system, even if sys is already a TransferFunction object.

tf(num, den)

Create a transfer function system from its numerator and denominator polynomial coefficients.

If num and den are 1D array_like objects, the function creates a SISO system.

To create a MIMO system, num and den need to be 2D nested lists of array_like objects. (A 3 dimensional data structure in total.) (For details see note below.)

tf(num, den, dt)

Create a discrete time transfer function system; dt can either be a positive number indicating the sampling time or ‘True’ if no specific timebase is given.

Parameters:

sys: LTI (StateSpace or TransferFunction)

A linear system

num: array_like, or list of list of array_like

Polynomial coefficients of the numerator

den: array_like, or list of list of array_like

Polynomial coefficients of the denominator

Returns:

out: TransferFunction

The new linear system

Raises:

ValueError

if num and den have invalid or unequal dimensions

TypeError

if num or den are of incorrect type

See also

ss, ss2tf, tf2ss

Notes

num[i][j] contains the polynomial coefficients of the numerator for the transfer function from the (j+1)st input to the (i+1)st output. den[i][j] works the same way.

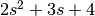The list [2, 3, 4] denotes the polynomial $2s^2 + 3s + 4$ .

Examples

>>> # Create a MIMO transfer function object
>>> # The transfer function from the 2nd input to the 1st output is
>>> # (3s + 4) / (6s^2 + 5s + 4).
>>> num = [[[1., 2.], [3., 4.]], [[5., 6.], [7., 8.]]]
>>> den = [[[9., 8., 7.], [6., 5., 4.]], [[3., 2., 1.], [-1., -2., -3.]]]
>>> sys1 = tf(num, den)

>>> # Convert a StateSpace to a TransferFunction object.
>>> sys_ss = ss("1. -2; 3. -4", "5.; 7", "6. 8", "9.")
>>> sys2 = tf(sys1)