control.ss

control.ss(*args)

Create a state space system.

The function accepts either 1, 4 or 5 parameters:

ss(sys)
Convert a linear system into space system form. Always creates a new system, even if sys is already a StateSpace object.
ss(A, B, C, D)

Create a state space system from the matrices of its state and output equations:

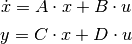
\dot x = A \cdot x + B \cdot u y = C \cdot x + D \cdot u

ss(A, B, C, D, dt)

Create a discrete-time state space system from the matrices of its state and output equations:

x[k+1] = A \cdot x[k] + B \cdot u[k] y[k] = C \cdot x[k] + D \cdot u[ki]

The matrices can be given as array like data types or strings. Everything that the constructor of numpy.matrix accepts is permissible here too.

Parameters:

sys: StateSpace or TransferFunction

A linear system

A: array_like or string

System matrix

B: array_like or string

Control matrix

C: array_like or string

Output matrix

D: array_like or string

Feed forward matrix

dt: If present, specifies the sampling period and a discrete time

system is created
Returns:

out: StateSpace

The new linear system
Raises:

ValueError

if matrix sizes are not self-consistent

See also

tf, ss2tf, tf2ss

Examples

>>> # Create a StateSpace object from four "matrices".
>>> sys1 = ss("1. -2; 3. -4", "5.; 7", "6. 8", "9.")

>>> # Convert a TransferFunction to a StateSpace object.
>>> sys_tf = tf([2.], [1., 3])
>>> sys2 = ss(sys_tf)