control.care¶

control.care(A, B, Q, R=None, S=None, E=None)¶

(X,L,G) = care(A,B,Q,R=None) solves the continuous-time algebraic Riccati equation

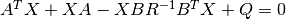
$A^T X + X A - X B R^{-1} B^T X + Q = 0$

where A and Q are square matrices of the same dimension. Further, Q and R are a symmetric matrices. If R is None, it is set to the identity matrix. The function returns the solution X, the gain matrix G = B^T X and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G.

(X,L,G) = care(A,B,Q,R,S,E) solves the generalized continuous-time algebraic Riccati equation

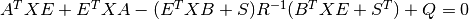
$A^T X E + E^T X A - (E^T X B + S) R^{-1} (B^T X E + S^T) + Q = 0$

where A, Q and E are square matrices of the same dimension. Further, Q and R are symmetric matrices. If R is None, it is set to the identity matrix. The function returns the solution X, the gain matrix G = R^-1 (B^T X E + S^T) and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G , E.