The second transformation is reflection which is similar to mirroring images.

Consider reflecting every point about the 45 degree line y = x:

Consider any point 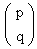. Its reflection about the line y = x is given by 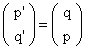, i.e., the transformation matrix must satisfy

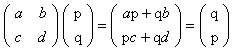
which implies that a = 0, b = 1, c = 1, d = 0, i.e., the transformation matrix that describes reflection about the line y = x is given by

What do you suppose the transformation matrix looks like for describing reflection about the line y = -x?

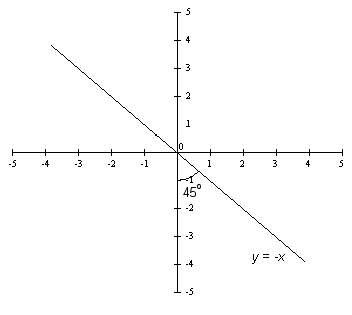
Reflections

Try reflection about the line y = x out on the rectangular diver in the plot.

Your browser is not Java capable.

This window shows the side view of a diver. The diver can be reflected by pressing "Transform". The elements a,b,c, and d of the matrix can be replaced arbitrarily and the diver will be transformed accordingly if "Transform" is then pressed. To return the diver to its initial condition press "Reset". The coordinates of a point on the graph can be obtained by clicking anywhere on the graph. The x and y coordinates will be displayed in the lower left hand side of the applet. To zoom in or zoom out, click the appropriate button.