| Previous | ToC | Next | Labs: Geometry and Motion Control. Part 1. | Math Alive |
Rotation
There are four simple linear transformations that can easily be described by multiplication of a 2 x 2 matrix. These types of matrices are used for many different applications, including in the computer graphics that you see in special effects at the movies.
The first is rotation.
Suppose that we want to find the 2 x 2 matrix that describes rotation of the diver by 90 degrees in the
counterclockwise direction. Consider first the line connecting  to
to 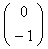 .
.
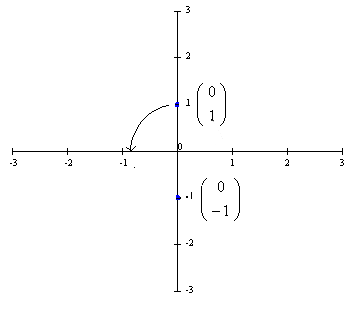
After rotating this line by 90 degrees in the counterclockwise direction (about the point  ) we
should get the new line connecting
) we
should get the new line connecting 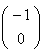 to
to
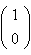 .
.

The 2 x 2 matrix that takes  to
to
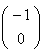 and
and 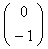 to
to 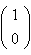 is given by:
is given by:
![]()
since
![]()
and
![]()
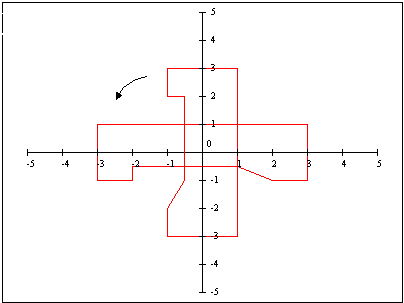
See what happens when we apply this transformation to every point on the diver.
More generally rotation of the line connecting  to
to
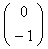 by
by
 degrees in the
counterclockwise direction takes us to
the new line connecting
degrees in the
counterclockwise direction takes us to
the new line connecting 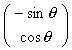 to
to
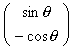 . And rotation of the line connecting
. And rotation of the line connecting
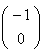 to
to 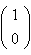 by
by
 degrees in the counterclockwise direction takes us to the new line connecting
degrees in the counterclockwise direction takes us to the new line connecting
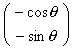 to
to  .
.
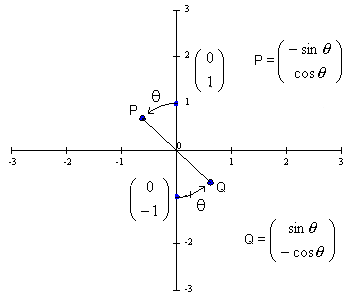
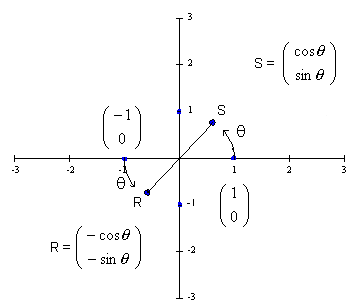
We can find the 2 x 2  transformation matrix as follows.
We need
transformation matrix as follows.
We need
 to be equal to
to be equal to 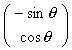 , i.e. b = -sin
, i.e. b = -sin  and d = cos
and d = cos  and we need
and we need
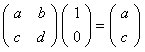 to be equal to
to be equal to  , i.e. a = cos
, i.e. a = cos
 and c = sin
and c = sin
 .
.
Thus, the rotation by  degrees in the counterclockwise direction about the point
degrees in the counterclockwise direction about the point
 on the plane is given the
transformation matrix:
on the plane is given the
transformation matrix:
![]()
Rotations
Try out various choices of q to see the rectangular diver rotate about the origin.
This window shows the side view of a diver. The diver can be rotated about the origin by entering the value of theta in the appropriate textfield and then by pressing "Transform". To return the diver to the original orientation press "Reset". The coordinates of a point on the graph can be obtained by clicking anywhere on the graph. The x and y coordinates will be displayed in the lower left hand side of the applet. To zoom in or zoom out, click the appropriate button.
| Previous | ToC | Next | Last Modified: August 2008 |