control.lqr

control.lqr(*args, **keywords)

Linear quadratic regulator design

The lqr() function computes the optimal state feedback controller that minimizes the quadratic cost

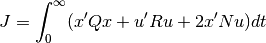
J = \int_0^\infty (x' Q x + u' R u + 2 x' N u) dt

The function can be called with either 3, 4, or 5 arguments:

  • lqr(sys, Q, R)
  • lqr(sys, Q, R, N)
  • lqr(A, B, Q, R)
  • lqr(A, B, Q, R, N)

where sys is an LTI object, and A, B, Q, R, and N are 2d arrays or matrices of appropriate dimension.

Parameters:

A, B: 2-d array

Dynamics and input matrices

sys: LTI (StateSpace or TransferFunction)

Linear I/O system

Q, R: 2-d array

State and input weight matrices

N: 2-d array, optional

Cross weight matrix
Returns:

K: 2-d array

State feedback gains

S: 2-d array

Solution to Riccati equation

E: 1-d array

Eigenvalues of the closed loop system

Examples

>>> K, S, E = lqr(sys, Q, R, [N])
>>> K, S, E = lqr(A, B, Q, R, [N])