A transformation of the plane assigns to each point on the plane a new location 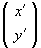on the plane. Application of the transformation to an object in the plane means each point of the object is moved to its new location. Depending on how dramatic the transformation is, the new image might be only a slightly modified version of the original plot or it may end up to be a very warped version. A photographic enlargement is a familiar example of a simple transformation. Distortions on a television screen or the "funny" mirror at Thomas Sweets are the results of more complicated transformations.

A linear transformation ensures that points that are originally in a straight line remain in a straight line even after they are transformed. The following assignment defines a linear transformation:

The point A = 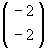is transformed into AA = 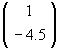and the point B = 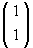is transformed into BB = 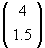. Check that the line connecting A to B transforms as shown in the figure, i.e., the points along the line connecting A to B are transformed into the points along the line connecting AA to BB.

For example, in the window below, if you click on a point along the line connecting A to B you will see the transformation of that point and this should lie along the line connecting AA to BB. The software will provide the coordinates of the original and the transformed points so that you can double check by hand that the transformation satisfies the assignment defined above. Try also clicking on the line from AA to BB.

Your browser is not Java capable.

Click on the either the line connecting points A and B or the line connecting AA to BB to see the original and transformed points appear on the plot. The coordinates of the original point and transformed point are given below the picture.