If we now go back and allow e and f to be nonzero, the complete transformation is given by

This uses our convenient matrix notation. However, there is an even more compact way to describe this transformation using a single 3 x 3 matrix. To do so we write each coordinate pair as a triplet with the third number in the triplet always equal to 1, i.e., becomes . Then, the 3 x 3 matrix in the following expression contains all of the information necessary to define the transformation:

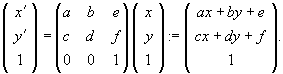
For example, the transformation that yields a shear along the x-axis with k = 2 and then a translation by 3 in the y direction is given by the matrix

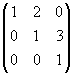
Practice
Computing Transformations

First try computing the transformation on a given point by performing the multiplication of the 3 x 3 matrix by the triplet.

Your browser is not Java capable.

Transformations

Now try out transformations and see how the diver transforms.

Your browser is not Java capable.

This window shows the side view of a diver. Click the appropriate radio button to enable the ability to enter theta, e, and f OR to enter a,b,c,d,e and f. Then press "Transform". To reset the diver to its original orientation, shape, size and position press the button marked "Reset". The coordinates of a point on the graph can be obtained by clicking anywhere on the graph. The x and y coordinates will be displayed in the lower left hand side of the applet. To zoom in or zoom out, click the appropriate button.

WARNING: When changing values in the a,b,c,d,e, and f textfields, be certain that the textfield is empty (i.e. all current text is deleted) before you enter new values. Otherwise you may submit different values than you actually want.