Now that we know how to perform linear transformations, we can perform several transformations, one after the other. The matrix notation gives a convenient means to keep track of the associated calculations. For example, suppose we first perform a counterclockwise rotation by = 90 degrees and then we perform a shear along the x-axis with k = 2. After the rotation we compute

.

The new coordinate pair is and so we apply the shear to these coordinates:

Since we know the expressions for x' and y' in terms of x and y from the rotation assignment, we can compute the final coordinate pair in terms of the original coordinates by substitution:

In other words,

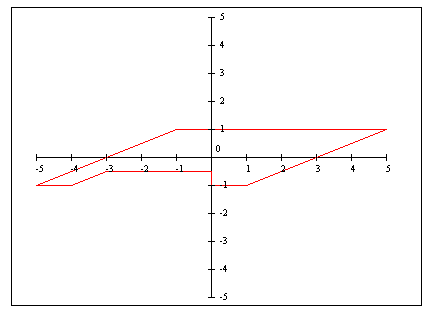
The net result of the rotation followed by the shear is shown in the plot.