| ToC | Next | Labs: Graph Theory. Part 1. | Math Alive |
Basics of Graph Theory
The basic objects in graph theory are graphs. A graph is a slightly abstract represention of some objects that are related to each other in some way, and of these relationships. The objects are drawn as dots called vertices; a line (or curve) connects any two vertices representing objects that are related or adjacent; such a line is called an edge. Generally, the edges are allowed to cross in a drawing (because it may be impossible to draw lines for all the relationships without ever crossing); the vertices are shown as fairly fat dots to distinguish them from just random edge crossings.
You find examples of graphs at the back of any airline in-flight magazine, in which vertices represent cities and with edges between any two cities which can be reached from each other by a non-stop flight. You can also make a graph for a sports championship, in which you use vertices to represent the teams, and you connect them (i.e. draw an edge between them) if and only if the two teams played against each other. Another example is given by social networks, in which we may represent people by vertices with edges linking any two friends, etc.
We will study only the so-called simple graphs. Simple graphs do not have edges that begin and end at the same vertex; they also don't have multiple edges between any two vertices.
Here are some examples.
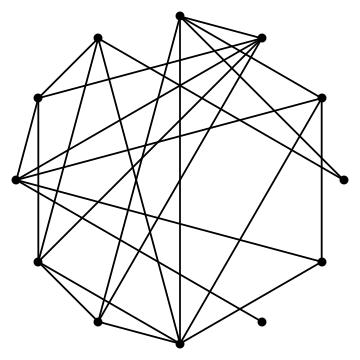
Here is a graph with 12 vertices and 24 edges.
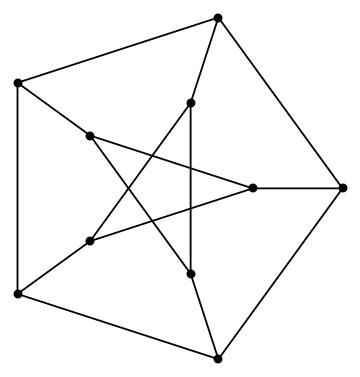
Here is the Petersen graph, dating back to the 19th century.
A graph is called connected if every vertex can be reached from any other vertext by traveling along edges. A simple graph doesn't need to be connected. If a vertex doesn't have any edges it is called an isolated vertex.
If a graph is not connected, it consists of several components. An isolated component is a maximally connected subgraph, i.e. a piece of the graph (some of the vertices of the original graphs, and all the edges of the original graph between those vertices) that is not connected to rest of the graph, but that is itself connected. How many components are there in the graph below?
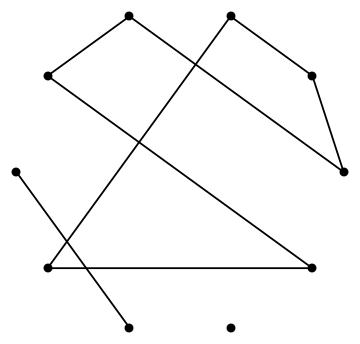
| ToC | Next | Last Modified: August 2008 |