Improving Non-Local Means operators
General Description
Non-Local Means is a patch-based method for denoising. The idea behind this denoising method is to average any given patch based upon similar patches from all over the image, regardless their locations (also known as neighborhood filtering). The operator is constructed by an affinity matrix, normalized to be row-stochastic. The noisy patches induce an affinity matrix contaminated with noise. Thus, filtering out the noise of the operator results in a low-rank, improved operator.
The implementation of the filter is efficiently done by Chebyshev polynomials for matrices. We demonstrate the method numerically on two data sets.
Clean Images data sets
Set 1 - 15 images of ~120X120.
Set 2 - 23 images of ~ 512X512.

Related publications
approximation. By Victor May, Yosi Keller, Nir Sharon, and Yoel Shkolnisky. In
IEEE Transactions on Image Processing
-
2.Matrix functions based on Chebyshev expansion and its application for subspace recovery. By Nir Sharon, and Yoel Shkolnisky. Coming soon.

Some numerical results
Comparison between denoising of NLM and our improved NLM methods, over natural images of ~0.25M pixels contaminated with Gaussian noise. On the right are the differences images, between the denoised images and their clean versions. Dark blue color stands for zero value pixel (perfect reconstruction).
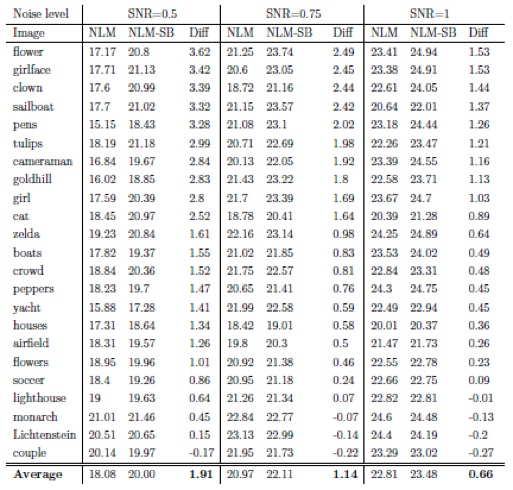
Full comparison between denoising of NLM and our improved NLM methods, over natural images of ~0.25M pixels contaminated with Gaussian noise. The data base includes 23 images and given below (Set 2). The results appear in PSNR (dB) and show that as the level of noise arise (lower SNR values) the improvement increases significantly (NLM-SB stands for our method).

We implemented a two-stages scheme, as suggested by Meyer and Shen. In this scheme, one computes and apply another operator over the denoised image. We show improvements for the NLM operator also in the context of this two-stages scheme (Here NLM-SB2 is applying naively two improved NLM operators and SB-Meyer is using our method in the two-stages scheme of Meyer and Shen).

BM3D is considered state-of-the-art in terms of PSNR gain for denoising. While PSNR is the standard method for measuring the error of denoising, some other criterions can be considered as well. For example, texture preserving.
