IAMP


Back to
OP page

Combined
List


List by
Contributors

Extended States

Contributed by: M. Aizenman (Princeton Univ.), Dec. 15, 1998.

Abstract   Establish the existence (in some energy range) of extended eigenstates, or continuous spectrum, for linear operators with extensive disorder. A prototypical example is the discrete Schroedinger operator with random potential



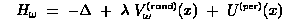
acting in l2(Zd), with:

      Delta -- the discrete Laplacian (n.n. difference operator),
      V(rand) -- a random potential, its values at the sites x forming a collection of independent identically distributed random variables, and
      U(per) -- a periodic potential (optional, its inclusion is not essential for the problem to be interesting).

Extended states play a basic role in elementary explanations of conduction in solid state. The scaling theory of AALR [1] suggests that such states do occur (almost surely for lambda small enough) in dimensions d > 2.
Nevertheless, despite continuing efforts, continuous spectrum (in the presence of extensive disorder) was established only for such random operators on homogeneous trees (Bethe lattices) [2].

A related open problem is to shed light on the situation in the borderline case (?) of d=2 dimensions.

The localized (pure-point) spectrum is better understood.
Some textbooks (with extensive reference lists) are listed under [3]. Among the many recent localization results are extensions to other wave equations [4], and bounds with applications to quantum Hall systems [5].

References:

  1. E. Abraham, P.W. Anderson, D.C. Licciardello, and T.V. Ramakrishnan: ``Scaling theory of lacalization: absence of quantum diffusion in two dimensions.'' Phys. Rev. Lett. 42, 673 (1979)

  2. A. Klein, ``Absolutely continuous spectrum in the Anderson model on the Bethe lattice,'' Mathematical Research Letters, 1, 399 (1993).

  3. H. Cycon, R. Froese, W. Kirsh, and B. Simon: Topics in the Theory of Schroedinger Operators (Springer-Verlag, 1987).

    R. Carmona and J. Lacroix: Spectral Theory of Random Schroedinger Operators (Birkhauser 1990).

    L. Pastur and A. Figotin: Spectra of Random and Almost Periodic Operators (Springer-Verlag 1992).

  4. A. Figotin and A. Klein, ``Localization of electromagnetic and acoustic waves in random media,'' J. Stat. Phys. 76, 985 (1994).

  5. M. Aizenman and G.M. Graf: ``Localization bounds for an electron gas.'' J. Phys. A: Math. Gen. 31, 6783 (1998).



Back to:   Open Problem page             

Mail comments to:

aizenman@princeton.edu