IAMP

Back to
OP page

Combined
List

List by
Contributors

Navier Stokes equations
global existence and uniqueness

Contributed by: Ya. Sinai (Princeton Univ.), October 5, 1998.

Abstract   Prove, or disprove, the global existence and uniqueness of solutions for 3D Navier Stokes systems. In the simplest case the system of equations has the form:

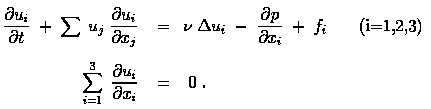
The unknown functions are ui(x,t) (i=1,2,3) and p(x,t), and it is natural to consider the case of periodic boundary conditions.

Question: Assume that the initial conditions, ui(x,0), are "smooth". Is it true that there exists a unique smooth solution for all t > 0 ?

The vast majority of experts believes that the answer is positive. In spite of this it is worthwhile to start with a construction of counter-examples.

References:

  1. A, Chorin: Vorticity and Turbulence (Springer-verlag, 1994).

  2. C. Doering, J. Gibbon: Applied Analysis of the Navier-Stokes Equations (Cambridge University Press, 1995).

  3. J. Mattingly and Ya.G. Sinai: "An elementary proof of the existence and uniqueness theorem for 2D-Navier-Stokes system", submitted to Annals of Math.

Back to:   Open Problem page             

Mail comments to:

sinai@math.princeton.edu (contributor), aizenman@princeton.edu (editor)