Let's say the car moves forwards and backwards along its long axis and sideways along its short axis. We begin by writing down the 3 × 3 matrices that represent a pure forward/backward translation P_f, a pure sideways translation P_s and a pure rotation P_r:

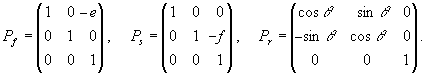
Note that, as explained earlier, these correspond to "motions of the world" with respect to the car driver; the x-axis remains fixed in the long axis direction of the car, and the origin (where x and y-axis intersect) remains in the center of the car. When the angle in P_r is positive, then the world as seen from the car veers to the right (clockwise rotation of world axes with respect to car axes), i.e. the car turns to the left; when the angle is negative, the opposite happens.

Likewise, when the translation amount e is positive, the "world" is going backward with respect to the car, or (more reasonably) the car is going forward with respect to the stationary world.

So let's look at the sequence: car turns left, drives forward so that its wheels roll over for β degrees, corresponding to traveling forward for a distance k, then the car turns right by the same amount that it turned left before, and it drives backwards for a distance k. This is given by the product of four matrices:

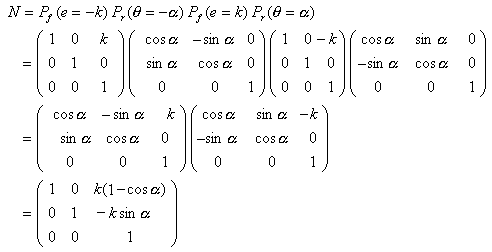
where we use the facts that sin(-α) = -sin α, cos(-α) = cos α and cos² α + sin² α = 1.

Recall that this transformation should be applied to the world axes (think of these axes as a figure) with repect to fixed axes on the car, i.e. the x-axis along the long axis of the car, and the y-axis along the short of the car.

If α is relatively small, i.e. smaller than 10 or 20 degrees, then cos α ≅ 1 and sin  α ≅ α. In this case

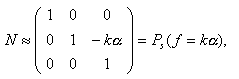
i.e., the result of the non-reciprocal sequence of four motions is a net sideways translation. Note also that the car moves sideways by an amount roughly equal to kα. If α is given in degrees then replace kα with kαπ/180. (For α large, there will also be some net forward or backward translation.)

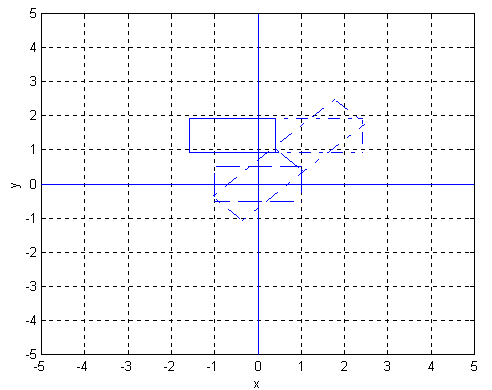
In the plot we show the result of such a sequence of maneuvers for e = k = 2 and θ = α = 45 degrees. The final position and orientation is given in solid lines. The intermediate steps are shown in dash-dot lines. Note that the maneuver looks like a jerky parallel park!