Problem 1. Maximize the Flow.

The Ford-Fulkerson algorithm is another name for the process of repeatedly finding augmenting paths and upping the flow by one unit along them that we saw in class. In this problem, we will use an online java applet http://www.cs.pitt.edu/~kirk/cs1501/animations/Network.html to get some practice with the Ford-Fulkerson algorithm.

a) Create a directed graph of at least 8 vertices and at least 12 edges of at least 5 different capacities. Make sure you designate a source vertex and a destination (target) vertex. Draw your graph in the space below and then use the online java applet to draw it. You will first need to use the add node command to place your vertices. Then you will use the add edge command and click on ordered pairs of vertices to add edges. Finally, adjust the capacity on each edge by adjusting the number under capacity on the side and then clicking the appropriate edge. Don?t forget to use the source and destination buttons to identify the source vertex and destination vertex.

b) Hit the step button once. This will find one augmenting path and increase the flow along it. Either print the result or draw the graph and label it with the resulting flow.

c) Keep running the algorithm on the applet until no additional augmenting paths can be found. Either print and attach the result or draw the graph and label it with the resulting flow.

d) Find the min cut of the graph that prevents the algorithm from finding any more augmenting paths.

Problem 2. Street Network

The following directed graph represents the road network between a city and a suburb of that city:

Each morning, most of the people in the suburb are trying to commute to their workplaces in the city, so we would like to be able to move as much flow as possible from the suburb (the source) to the city (the destination).

a) Find the min cut for this graph. Highlight or otherwise indicate the edges that go from the source's group of vertices to the target's group of vertices in the min cut. What is the capacity of this cut? What is the maximum feasible flow for this network?

b) Suppose you are given the job of building a new road to shorten everyone?s morning commute. The road can have a capacity of up to three and can connect any two vertices. Where would you place this road? What is the new min cut? What is the maximum feasible flow of the new graph?

c) Explain why traffic in cities often backs up at bridges in terms of the max flow, min cut theorem (Thm 3 in the first week's notes).

You and your friends Amy, Ben, Christine, Dan, and Emily are going to the movies. You want to take the least number of cars possible, but Ben refuses to be in the same car with any of your female friends and Dan refuses to be in the same car with Ben or Emily.

a) Draw a graph describing the conflicts.

b) What does the greedy coloring theorem allow you to say about the minimum number of cars you can take?

c) What is the actual minimum number of cars you can take? Please give an actual assignment of people to cars that resolves the conflicts for this minimum number of cars and explain what prevents you from taking one fewer car than this minimum.

Problem 4. Coloring Trees

All trees are planar graphs, so Appel and Haken's celebrated result tells us that they can be colored properly with four or fewer colors.

We think we can do better. Can all trees be colored with three or fewer colors? Can all trees be colored with two or fewer colors? Give a general procedure that colors a tree with the minimum number of colors, and explain why your procedure works.

Draw a small tree (10-20 vertices) and demonstrate your procedure with that tree.

Problem 5. Complete Graphs

The complete graph on N vertices, denoted by K_N, is a graph with N vertices in which each pair of vertices is joined by an edge. We do not have multiple edges between the same pair of vertices, nor do we have loops in K_N.

Some of the graphs K₁, K₂, K₃, K₄, K₅, K₆, and K₇ can be drawn in a plane without any edges crossing over each other, and some will always have at least one edge crossing over another no matter how we try to draw them. Which of these seven graphs can be drawn without edges crossing (recall that you can draw edges curved), and which of the graphs cannot be drawn without edges crossing? If you say that a graph can be drawn without edges crossing, furnish such a drawing to prove your claim. If you say that a graph cannot be drawn without edges crossing, you need to prove that it cannot be done, no matter how you try to do it. Since there are infinitely many ways to try to draw a graph, you cannot justify your claim by simply saying that you tried but did not succeed. Rather, you need to provide a justification. Hint: use Appel and Haken's result that all planar graphs are 4-colorable.

Problem 6. Coloring Polygons

Suppose that N is an integer greater than 1. What is the chromatic number of a polygon with N sides? Does your answer depend on N?

Problem 7. 2-Colorable Graphs

Recall that we always assume that our graphs are connected unless explicitly noted otherwise. All graphs in this problem are assumed to be connected.

(a) First warm up: Which (connected) graphs are 1-colorable? Can you classify them all?

Second warm up: By an odd polygon, we mean a polygon with an odd number of sides. Show that a graph containing an odd polygon is not 2-colorable. (Hint: See the previous problem.)

(b) Draw a graph (with 10-12 vertices) that is not a tree and has no odd polygons. Color one vertex blue. Now color the rest of the vertices properly using only blue and red. You should find that you are able to do this, but that there is only one way to do this (i.e., each vertex has a color assignment forced upon it after you color the first vertex blue). Is there a succinct rule that which tells you what color a vertex must receive?

(c) Come up with a general procedure for coloring graphs without odd polygons. Your procedure should always properly 2-color such a graph. You should explain why your procedure never fails to work.

Problem 8. Plato and Euler

4) It is an interesting fact that any graph that represents the corners and edges of a simply-connected three-dimensional solid can be drawn as a planar graph. The resulting planar graph is called a planar embedding of the solid.

So, for example, we can find a planar embedding for the tetrahedron by taking the base of the pyramid and stretching it out until we can fit the other three edges inside:

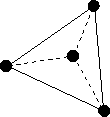
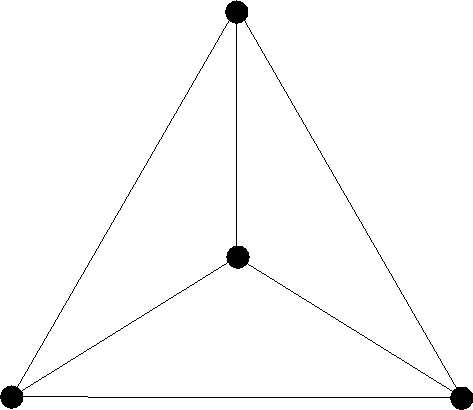
Note that the resulting two-dimensional graph is isomorphic to the graph in three dimensions.

a) Draw a planar embedding of a cube.

The pyramid and the cube each have some interesting features. Each face is the same regular polygon (one in which all sides and angles are the same) and the number of these faces that meet, as well as the angles at which they meet, are the same at each vertex. For example, each face of the pyramid is an equilateral triangle and exactly three such faces meet at each of the four vertices.

It can be shown using the Euler characteristic (see Challenge Problem #3) that there are only five solids with these properties. The remaining three are:

The octahedron, a solid with 8 triangular faces, four of which meet at each vertex: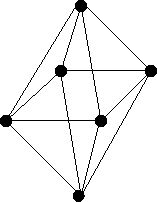
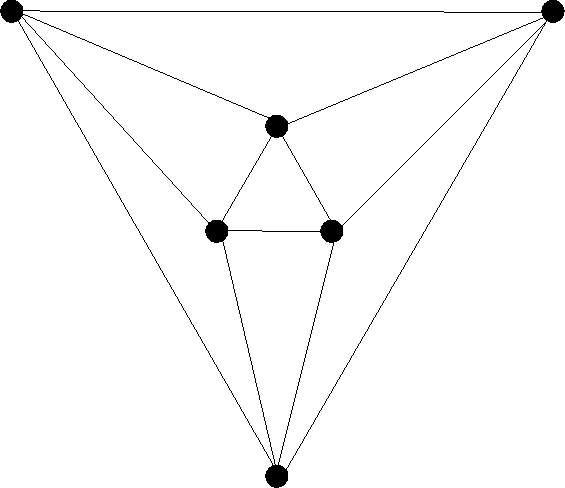
The dodecahedron, a solid with 12 pentagonal (5-sided) faces, three of which meet at each vertex, can be viewed at MathWorld, and here is the graph: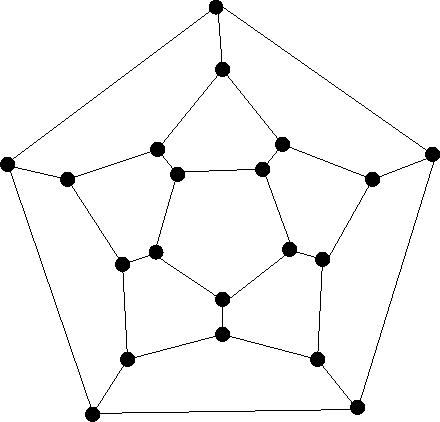
The icosahedron, a solid with 20 triangular faces, five of which meet at each vertex, can be viewed at MathWorld, and here is the graph: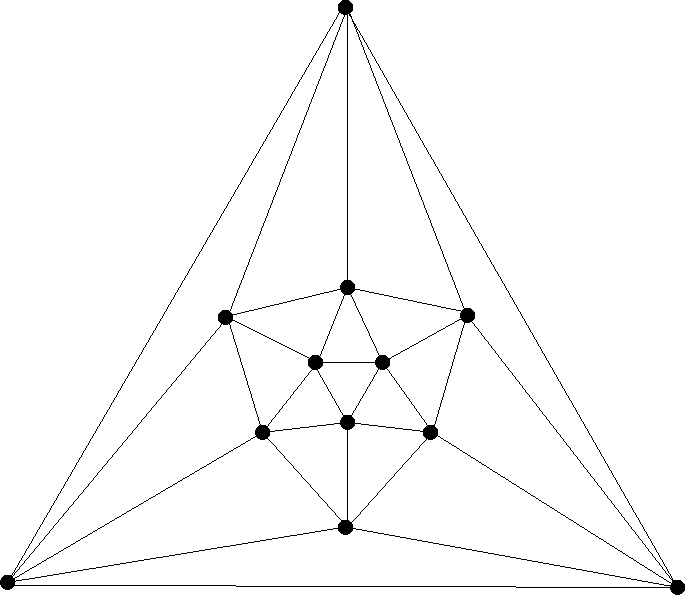

Knowledge of the platonic solids goes back thousands of years to the ancient Greeks. Plato proposed that four of these five solids were associated with the four elements: fire, earth, air, and water. Moreover, much in the same way that we believe today that all matter is made from the basic chemical elements in the form of tiny atoms, he believed that all matter was made of these four elements in the form of tiny platonic solids. Aristotle introduced the idea of a fifth element, aether, which was associated with the dodecahedron by Philolaus. We should note that modern chemistry shows that many chemical compounds have molecules with tetrahedral and octahedral shapes.

b) Find the chromatic number of each platonic solid. For each solid, provide a coloring of the associated graph that uses exactly this many colors and briefly explain why you can?t use fewer colors.

c) Count the number of vertices, edges, and faces for each platonic solid and show that each one satisfies the Euler characteristic. (Don't forget to count the unbounded face if you choose to count faces using the planar embeddings.)

d) Could we have a Platonic solid with 18 seven-sided faces and 30 vertices? How about one with 18 five-sided faces and 30 vertices? (Hint: Since each edge is where two faces meet and each face has five sides, how many edges are there in the graph for this solid?)

e) Will all solids satisfy the Euler characteristic? Explain why or why not.

Problem 9. Disconnected Countries

In our original map-coloring problem, we assumed that every country is a connected mass of land, and we wanted to color adjacent countries with different colors. (Countries that only touch corner-to-corner were not counted as adjacent.)

Now we look at the map-coloring problem that is in all respects the same, except that now we allow the possibility that a country is made up of multiple disconnected masses of land. We insist that all the various patches that make up a country be colored the same color in our coloring. As usual, when two territories belonging to different countries are adjacent (not counting corner-to-corner touching as adjacency), we insist that they receive different colors.

Do six colors suffice to color every map in this more general situation? If so, explain why. If not, then furnish a map that is not 6-colorable, and make sure you name your countries (single-letter names will suffice) and label each territory with the letter of the country to which it belongs.

Problem C1.

Suppose that you have a transportation network as defined in the lecture notes. In the notes we showed that the maximum achievable net flow is always less than or equal to the capacity of a mincut. The big claim (stated, but not proved, in the notes) is that the maximum achievable net flow is actually equal to (not less than) the capacity of the mincut in all cases. Prove this equality. (Hint: Show that if the net flow in a flow assignment is less than the mincut capacity, then there MUST be an augmenting path connecting the source vertex s to the target vertex t.)

Problem C2. Coloring Doughnut Maps

Our theorems about map coloring all assume that our map is drawn on a plane (they also work just as well if the map is drawn on the surface of a sphere). But Planet X is a torus (doughnut-shaped) astronomical object:

Suppose we have a regular polyhedron where each face has p sides (edges), and where q faces meet at each vertex. Using the Euler formula, v-e+f=2, prove that (1/p)+(1/q)=(1/2)+(1/e). Use this to show that there are only five regular polyhedra.